Tutorial 4 - fMRI Preprocessing and Quality
Goals
Understand how preprocessing can be used to improve our statistics
To understand the types and causes of motion artifacts
To understand the benefits and limitations of motion correction algorithms
To become familiar with a variety of spatial and temporal smoothing methods
To understand the logic of including predictors of no interest in the presence of motion artefacts and linear drift
Accompanying Data
Tutorial outline
fMRI data is noisy by nature, meaning that many changes in the signal intensity are due to factors other than the BOLD response to our protocol. This variability can arise from physical noise, especially on low-field scanners (e.g., 1.5T) or scanners that do not undergo regular quality assurance testing. It can also arise from physiological noise, which includes factors related to the participant such as head and body motion, breathing and cardiac pulsations, as well as performance factors such as fluctuations in alertness.
To increase the signal-to-noise ratio and improve our stats, several strategies are available. In the first part of this tutorial, you will see how preventing and correcting for motion artefacts can help reduce noise. In second part of this tutorial, you will see how spatial smoothing and temporal filtering can also help improve the signal-to-noise ratio.
Background on Motion Artefacts
Recall that head motion leads to several problems with fMRI data.
Voxels shift over time
Head motion can lead to artifacts in time courses (e.g., drift, spikes)
Motion of the head (or any other mass) changes the magnetic field, leading to artifacts.
There are three approaches to dealing with head motion artifacts:
A. Prevent it.
B. Correct it with preprocessing (motion correction)
C. Reduce the contamination of the time courses and reduce the residuals by including motion parameters as predictors of no interest
Motion-corrected data is never as good as data that didn’t have motion to begin with; therefore, do not underestimate the value of the first approach (A). Motion correction algorithms (B) reasonably well at shifting voxels back to the appropriate location, solving problem #1. Motion correction algorithms will often reduce the severity of problem #2. Including motion parameters as predictors of no interest (C) can lead to better estimates of activation levels (i.e., beta weights) and can reduce residuals, improving statistical power. None of these approaches (A, B or C) addresses problem #3 well. Emerging solutions for data collection (multi-echo imaging) show some promise for reducing the impact of problem #3 and will be discussed when we discuss MR physics.
Figure 5-1. Motion of a rigid body (like the head) in 3D space can be quantified and corrected using 6 motion parameters (3 translations and 3 rotations)
Motion Correction Algorithms
Motion correction algorithms attempt to correct the first two problems. These algorithms realign each volume (set of slices at one point in time) with a reference volume (often the first volume within a run) using 3 translation and 3 rotation parameters (Figure 1).
Figure 5-2. Recall that GLM stats can be improved by increasing the fit of the POIs, reducing residuals, and shifting known sources of noise into the GLM by adding PONIs.
Adding Motion Parameters as Predictors of No Interest to the GLM
Recall that statistical significance depends on how well the predictors of interest (POIs) fit the data relative to the residuals. By reducing noise, motion correction can help achieve more accurate estimates of beta weights (orange arrow) and reduce residuals (yellow arrow). However, because motion correction is imperfect, it is often beneficial to account for variability related to head motion using predictors of no interest (PONIs) in the GLM (red arrow). Shifting variance from the residuals to the model improves statistical significance.
This is a good solution so long as motion predictors are not highly correlated with our activation predictors (e.g., if they are due to things like swallows that are unrelated to the paradigm). If the motion PONIs and condition POIs are tightly correlated (e.g, in block-design studies of hand actions or speech), the situation is more complex.
General Instructions
The data for this tutorial includes one localizer run for each of two participants (P06 and P13). One or both of the participants have substantial head motion artifacts. In the first part on motion artefacts, you will evaluate each of the participants’ data for signatures of head motion. In the second part on motion artefacts, you will pick the participant that you think had the worst head motion artifacts, and compare different GLMs with and without predictors of non-interest (motion predictors).
Inspecting data for motion artefacts
There are three ways to inspect data for possible motion artefacts. For each participant in Tutorial 4, utilize the three approaches below to inspect the data for motion. Note the volumes (time points) at which funky things happened.
First, we will open the participant's functional 2D files by clicking on File/Open… command and selecting a .fmr file. For Step 1, choose the file that does not have motion correction applied, sub-XX_ses-01_task-Localizer_run-01_bold_SCCTBL.fmr where XX is the participant number.
Use the buttons on the left side of the main BV window to adjust rows and columns such that the matrix fills the screen. The bigger the slices, the better.
a) To play a movie of slices over time
Select Options/Time Course Movie… Click on “Preload All” to make your movie play more smoothly.
Use the bottom buttons to play the movie >, pause ||, step back < or step forward >|
You can also place your cursor in the numbered window right of “Time point:” and use the up and down arrows on your keyboard to move back and forward. You can click First <-> Last to jump between first and last volumes.
Figure 5-3. To play a movie for an .fmr file, go to Options/Time course movie
Figure 5-4. Time course movie controls
Some slices are more informative than others, especially the top slice of the brain, where up-down movements (z translation) is most easy to detect. Thought question (does not need to be answered in assignment): Why do you think this is?
While looking at the movie, note any time points at which things appeared “funky”. If you think you see motion artifacts, you should also examine the movie for the motion-corrected fMR to see if motion correction fixed it.
b) To see motion correction output
Select Analysis/General Linear Model: Single Study… Select Load… and select the file ending in _3DMC.sdm . Click “Use protocol” under Time course segmentation to see the colored bars showing the timing of conditions.
Figure 5-5. Loading predictors for a Single-Study GLM
Figure 5-6. The “Load” button allows you to view motion parameters
If you want to see the name of each predictor, under Predictors you can step through each of the six. To see them all at once, turn on “Show all” Note any time points where there were abrupt changes. Note any gradual changes. Pay attention to the magnitude of changes (y-axis)
c) Voxel surfing
Sometimes you can detect motion artifacts simply by looking across strategically or even randomly selected time courses.
To do so with .fmr files, click and drag the mouse to draw box containing the voxels for which you want to extract a time course . This will derive the time course from all voxels inside the brain in the box on that slice.
You can inspect the time course for suspicious trends across different regions of the brain (hint: try top and bottom slices, ventricles, outside head, regions of expected activation such as occipital pole.
Figure 5-8. You can select an entire slice to see the average time course of all voxels (above a certain intensity that corresponds to the voxels inside the brain)
Figure 5-9. Example time course, showing motion artifacts. Can you spot one “spike” and one “glitch”?
Question 1: a) Where would you expect to see genuine activation?
- Grey matter
- White matter
- Ventricles
- Near the edges of the head
- Grey matter
- White matter
- Ventricles
- Near the edges of the head
Question 2:
For each participant,
a) What evidence is there for gradual or abrupt head motion (and if abrupt, at which time points is the problem most evident)? If you think there is substantial motion, list all the signatures of the problem that led you to this conclusion.
b) For participants who show evidence of head motion, what could they have been doing to cause these artifacts?
Question 3: Which out of the two participants shows the most problematic data? Justify your choice.
Now let's see how well motion corection did at fixing the problems. Close all files. For the participant that had the worst motion, load the motion-corrected .fMR file (ending in 3DMCTS: sub-XX_ses-01_task-Localizer_run-01_bold_SCCTBL_3DMCTS.fmr). Play the movie and do some voxel surfing.
Question 4: How well did the motion correction work?
Question 5:
a) Many people assume that motion correction is a panacea (cure-all) for head motion. Is it? Why or why not?
b) Many researchers will exclude participants' data using some vaguely defined motion criterion like, "Data in which head motion exceeded 2 mm or 2 deg were excluded from analysis." Why is this too vague? When might such a statement indicate too much caution? When might it indicate not enough?
Close all files once you have completed this section.
Investigating Statistical Maps to Find Evidence for Artifacts and Evaluate the effect of Motion PONIs
After inspecting both participants' data, pick the participant that you think had the worst head motion artifacts and complete the folowing sections (a and b) for this participant (and only this participant).
a) Inspecting statistical maps can also provide clues as to the effect of head motion
In the previous section, you saw that you can inspect data for motion artefacts using time course movies, motion correction outputs and voxel surfing. However, you can also find evidence of motion when inspecting statistical maps. To do this, we will inspect what blobs appear on statistical maps when contrasting POIs vs baseline, and PONIs vs baseline.
1) Go to File/Open… and open the .fmr file without motion correction (sub-XX_ses-01_task-Localizer_run-01_bold_SCCTBL.fmr).
2) Go to Analysis/Overlay General Linear Model… and load the version of the GLM with both POIs and PONIs (sub-XX_ses-01_Localizer_run-1_POI+PONI.glm).
3) Set the contrast to the contrast shown in figure 5-10 (left), click OK and inspect which areas have significant activation.
4) Repeat the previous step (go to Analysis/Overlay General Linear Model…) and set the contrast to the contrast shown in figure 5-10 (right), click OK and inspect which areas have significant activation.
You can adjust thresholds by clicking these symbols (bigger blobs and smaller blobs) on the left side of the main BV window or by using the menu generated from Analysis/Overlay Volume Maps… (Analysis tab) (the latter shows you the Min threshold, which is helpful – for casual data inspection, Min = 2.5 or 3 is a reasonable value).
Question 6: Where do you see signals predicted by POIs? Where do you see signals predicted by PONIs?
Figure 5-10. Left = A typical contrast using only POIs. Right = a contrast using PONIs. Although PONIs, by definition, are generally not of particular interest, nevertheless, performing such contrasts can give you an idea of how problematic head motion is and which brain regions might be particularly vulnerable. You can also inspect the time courses of the artifact regions to see how bad the effects are.
Close all files once you have completed this section.
b) To contrast the effect of including PONIs in the data from the participant with the worst motion artifacts
Now, we will compare the statistical maps with POIs to statistical maps with POIs+PONIs.
1) Go to File/Open… and select the motion corrected file: sub-XX_ses-01_task-Localizer_run-01_bold_SCCTBL_3DMCTS.fmr. Do this again so you have two versions that you can jump between.
2) In one version (first tab), go to Analysis/Overlay General Linear Model… and select the file that includes only POIs (without PONIs): sub-XX_ses-01_Localizer_run-1_SCCTBL_3DMCTS_POI.glm. Contrast all 4 POIs vs. baseline (+1 +1 +1 +1).
3) In the other version (second tab), go to Analysis/Overlay General Linear Model… and select the version with both POIs and PONIs sub-XX_ses-01_Localizer_run-1_SCCTBL_3DMCTS_POI+PONI.glm. Contrast all 4 POIs vs. baseline (+1 +1 +1 +1).
Before comparing the two maps, go to Analysis/Overlay Volume Maps… to be sure that both versions are using the same statistical threshold.
Now, compare the two maps by toggling between the two tabs (you can also go to Window/Sub_Window View mode to see the two maps side by side).
Question 7:
a) How did the model with only POIs compare to the model with both POIs and PONIs?
b) Considering how the GLM works, what effect should the addition of PONIs have on statistical significance and why?
Question 8:
a) Explain three reasons that motion can be detrimental to fMRI data.
b) In general, which consequences of motion are fixed by motion correction algorithms and which are not?
c) Suggest three strategies that can be used to prevent head motion rather than correcting for it in adults and/or children.
Close all files once you have completed this section.
Spatial and temporal filtering
fMRI data can noisy in two ways: spatially and temporally.
Spatial noise is often a concern for anatomical images because noise across different voxels can make the images look grainy and make it harder to discern tissue types (e.g., gray vs. white matter).
Temporal noise is especially relevant for functional MRI. Temporal noise refers to changes in signal intensity over time that are due to factors other than the BOLD response to our protocol. This type of variability can arise from physical noise or physiological noise.
You have already seen in the previous section how motion correction can typically, but not always, reduce noise. Even when correction is not fully successful, including motion parameters as predictors of no interest can "soak up" variance due to motion and thus improve statistics. In this next part, you will see how spatial smoothing and temporal filtering preprocessing steps can also improve the signal-to-noise ratio.
Background on Spatial Smoothing
Figure 5-11. A Gaussian filter is characterized but the full-width at half maximum (FWHM).
During spatial smoothing, for each volume (time point), each voxel’s intensity is computed as a weighted average of its own intensity and the intensities of its neighbours within a set radius. The closer the neighbouring voxel, the more it contributes to the new intensity. The weights are determined by a Gaussian function and its size is characterized by its width at a y-value = half its height, which is called the full width at half maximum (FWHM) of the smoothing kernel (Figure 5-11).
If the noise is at a finer spatial scale than the signal, spatial smoothing improves data quality because genuine differences in intensity summate while noise differences cancel out. Figure 5-12 is an example of this. The BEFORE photo shows a grainy image that is due to noise related to taking a photo in dim light. The AFTER photo shows how spatial smoothing can make the picture look better. Adjacent pixels share differences in intensity (e.g., the cloud pixels are darker than sky pixels) but noise also leads to speckles (more fine-scale differences in intensity). When intensity levels for each pixel are smoothed through a weighted combination with neighboring pixels, differences in signal reinforce one another (e.g., dark cloud pixels are combined with other dark cloud pixels; light with light) while differences due to noise cancel one another out (a noisily bright pixel will be next to other pixels with lower intensities).
Figure 5-13. One functional data slice with different smoothing options.
Figure 5-13 shows a slice of functional data without smoothing (left), with 4-mm FWHM smoothing (centre), and with 8-mm FWHM smoothing (right). Notice the effects of the increasing the smoothing kernel. Note that some smoothing (4 mm) blurs out the speckles, making it easier to see gray vs. white matter differences while heavier smoothing begins to blur out gray and white matter together.
Spatial smoothing is also beneficial for reducing temporal noise. Adjacent voxels likely share temporal signal (e.g., a voxel that responds strongly when faces are shown is likely to be next to other voxels with a similar preference) but not temporal noise (especially physical noise). Spatial smoothing makes time courses cleaner because signals reinforce one another while noise cancels.
Spatial Smoothing in BrainVoyager
We have taken one run of the Localizer from one participant and applied different levels of spatial filtering to the data. We have also selected a peak voxel in the FFA and LOTC hand regions of interest. You will examine the maps to see how the data are affected by different types of filtering.
Figure 5-14. A file with multiple maps of the same contrast (Faces - Hands) after different combinations of spatial smoothing and temporal filtering.
1) Select File/Open , and open the anatomical file sub-03_ses-01_T1w_IIHC.vmr
2) Select Analysis/ Overlay Volume Maps , and then load multimap_final.vmp .
You will see that 6 maps have been created for you. All of these maps have been generated from a contrast of (+1 x Faces) + (-1 x Hands) such that face-selective areas will appear in the orange-yellow spectrum and hand-selective areas will appear in the blue-green spectrum (if you are using the classic look-up table).
All of the maps have been set to the same statistical cutoffs (minimum t = 3; maximum t = 6) to enable "apples to apples" comparisons between maps. Pay attention to the first four maps for now. These are an unfiltered run (with slice time - SCCTCBL - and motion - 3DMCTS - correction) and three levels of spatial smoothing (SS4, SS8, and SS12, where the number indicates the FWHM of the Gaussian kernel).
3) Toggle between the first four maps by clicking the box to the left of the map name until a plus sign appears beside the map you want to view. Pay particular attention to regions around the expected location of FFA and LOTC hand as well as to the "schmutz" (voxels that are in regions where no BOLD signal is possible/likely).
Question 9:
a) What effect does spatial smoothing have on the appearance of the maps?
b) Is more smoothing necessarily better? Select all that apply.
- More smoothing is always better.
- More smoothing can silence important voxels.
- More smoothing can wash out the singal of interest with irrelevant signal.
- More smoothing can lead to losing activation hot spots.
Now let's compare how spatial smoothing affects the time course of single voxels.
Figure 5-15. How to load an ROI/VOI file.
4) Go to Analysis/Region-of-Interest Analysis and load FFA+LOTChand.voi. This file contains the spatial locations of two voxels, one in FFA and one in LOTChand. By defining each voxel as a region of interest, we can ensure that, as you inspect different time courses, they will be based on the same voxel.
For each voxel, you can select the name and then click "Show VOIs". As you do so, the crosshairs will jump to that voxel's location in 3D space. (Note that the left side of the ROI dialog box has a list of files under Time Course (VTC) files.) Unfortunately because of the way BrainVoyager stores file paths, the paths will be incorrect for your data. Remove each of the files and add them in the following order - you might not see the vtc files - in this case just add the vtc files one at a time.
- sub-03_ses-01_task-Localizer_run-01_bold_SCCTBL_3DMCTS_256_sinc3_2x1.0_NATIVE.vtc
- sub-03_ses-01_task-Localizer_run-01_bold_SCCTBL_3DMCTS_256_sinc3_2x1.0_NATIVE_SD3DVSS4.00mm.vtc
- sub-03_ses-01_task-Localizer_run-01_bold_SCCTBL_3DMCTS_256_sinc3_2x1.0_NATIVE_SD3DVSS8.00mm.vtc
- sub-03_ses-01_task-Localizer_run-01_bold_SCCTBL_3DMCTS_256_sinc3_2x1.0_NATIVE_SD3DVSS12.00mm.vtc
For the voxels in FFA and LOTChand, step through each of the first four time courses (NATIVE, FWHM = 4; FWHM = 8; FWHM = 12).
Question 10: How does spatial smoothing using smaller and larger kernels affect the timecourse?
Temporal filtering
Using Fourier analysis, any time series (such as an fMRI time course) can be broken down into a series of sine waves. This is very useful for time series analyses because different sources of noise can occur cyclicly predominately in particular frequency bands. For example, outdoor temperature as a function of time (say over 20 years) would show cycles related to time of day (1 cycle/24 hours), time of year (1 cycle per year), and long-term climate changes (slow drifts), in addition to ~random fluctuations related to everyday weather.
fMRI data tends to have high noise in particular frequency ranges:
- Very low frequencies related to scanner drift and participant relaxation
- Frequencies related to breathing: ~0.3 Hz = 0.3 cycles/s [to calculate the period of a sine wave, take 1/frequency: (1/(0.3 cycles/sec)) = 3.3 s/cycle]
- Frequencies related to heart rate: ~1 Hz = 1 cycle/sec [= 1 s/cycle = ~60 beats/min]
Figure 5-16. For simple two-condition protocol, it is easy to predict the predominant frequency of activation.
In addition, good fMRI data will have legitimate BOLD signals at the frequency (or range of frequencies) of the paradigm. For simple designs (off-on-off-on…), as shown in Figure 5-16, this is easy to calculate. For example, if you have a run of 340 s with 16-s periods of off and on, you would have 10.5 cycles/340 s (Note, the extra half cycle comes from the black period at the end; if it ended at the end of the last pink cycle, there would be exactly 10 cycles). To compute the expected stimulation frequency in Hz: 10.5 cycles/340 s = 0.03 Hz.
Figure 5-17. For more complex, multi-condition protocols, the expected stimulation frequencies may be more complicated.
For designs such as the localizer data (Figure 5-17), which do not have precisely consistent periods (e.g., the time between the first and second pink epochs is shorter than the time between the second and third ones), you would not expect such straightforward paradigm-related frequencies. Nevertheless, since we have 4.2 cycles of stimulation for each condition, you would expect stimulus related activation to be around 4.2 cycles/340 s = ~0.012 Hz.
One strategy for improving fMRI statistics is to filter out frequencies outside of the expected paradigm frequencies. By removing noise at these frequencies, the residuals become smaller and thus our statistics improve.
Linear trend removal
The simplest temporal filtering we can do is to filter out any linear drifts in our data.
Widget 5-1 allows you to "fix" linear trends in two ways. Let's look at the GLM without either correction, with correction through linear trend removal (preprocessing), and with the linear trend removed through a PONI.
Use only the leftmost slider and the constant slider (keep the PONI slope at zero) to approximate the best fit beta weights for Voxel B when the linear trend is uncorrected. Note the appearance of the residuals and the magnitude of the sum of squared error.
Next, go back to the data above. Turn on "Linear Trend Removal" and re-fit the GLM . You can do this manually or use the Optimize GLM button. Note the appearance of the residuals and the magnitude of the sum of squared error.
Next, turn off "Linear Trend Removal" and re-fit the GLM, including the PONI slope slider . You can do this manually or use the Optimize GLM button. Note the appearance of the residuals and the magnitude of the sum of squared error.
Question 11: How did the residuals and squared error change after linear trend removal? Was one approach to dealing with linear trends better than the other?
High Pass, Low Pass and Band Pass Filtering
Another way of doing temporal filtering is by doing either high pass, low pass or band pass filtering.
- High pass: filters out the lowest temporal frequencies in our data allowing the high frequencies to pass through the filter.
Software defaults will typically filter out changes slower than 2-3 cycles/run (These values in Hz will depend on your run duration and will be very slow, e.g., 3 cycles/340 s = 0.009 Hz). High pass filtering also filters out linear trends so adding linear trend removal is redundant (You can think of a linear trend as being an ultra-low frequency -- imagine a sine wave wider than your screen with the upward or downward slope crossing though your time course).
- Low pass: filters out the highest temporal frequencies in our data, allowing only the low frequencies to pass through the filter.
One way to to this is to smooth the time course data with a Gaussian kernel over time. This technique is very similar to Gaussian spatial smoothing. A smoothing kernel is applied over each time point in a voxel’s time course. But instead of computing the weighted average of neighbouring voxel intensities at the same time, temporal smoothing computes those averages over time, using neighbouring time points.
- Band pass: filters out both low frequencies and high frequencies, we are allowing only an intermediate band of frequencies to pass through.
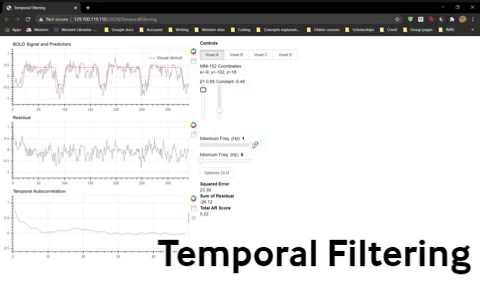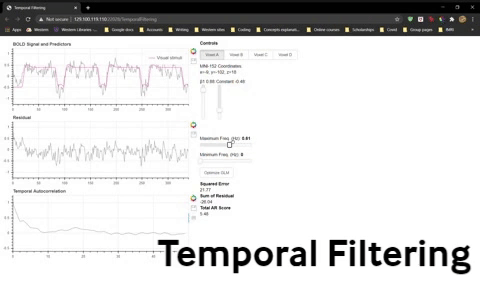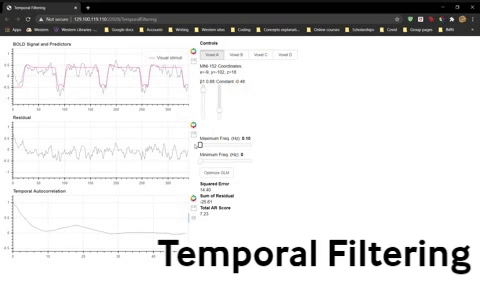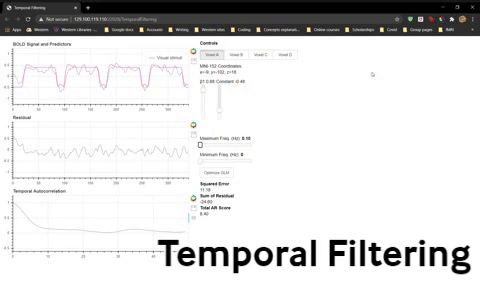
Let’s explore band-pass filtering using the following widget. Two sliders, Minimum Freq. and Maximum Freq. have been added to control which frequency components are allowed to contribute to the signal.
To perform high-pass filtering, set the minimum frequency to remove frequencies below that value.
To perform low-pass filtering, set the maximum frequency to remove frequencies above that value.
To do band-pass filtering, set minimum and maximum frequencies to remove frequencies at either extreme.
1) Fit the GLM (use Optimize GLM if you like) for Voxel 1 and note the beta weights, squared error, and pattern of residuals. Adjust the Minimum Freq slider to 0.01 Hz (without adjusting the Maximum Freq slider just yet). This means you are filtering out any frequencies below 0.01 Hz (and passing any frequencies above that cutoff). Refit the GLM and again note the beta weights, squared error, and pattern of residuals.
Question 12: What effect did this have on your data and what would be the consequences to your statistical significance?
2) Now try higher values for the minimum frequency (e.g. 0.1 Hz) and refit the GLM to see what effect it has.
Question 13: What are the consequences of aggressive high-pass filtering and why?
3) Set the Minimum Freq to 0.01. Now see what effect changing the Maximum Freq has on your data and model fits. (Note: The maximum frequency our data can have is 1 Hz because we sampled with a TR = 1 s, so we cannot filter out a Maximum Freq > 1 Hz.)
Question 14: Fill in the blanks. By changing the maximum frequency allowed in the signal, we are doing (high pass/low pass/band pass) filtering. Changing the maximum frequency makes the time course (smoother/noisier).
Question 15:
a) What happens if you set both Maximum Freq and Minimum Freq to 0.1 Hz? Why?
b) What type of filtering is this?